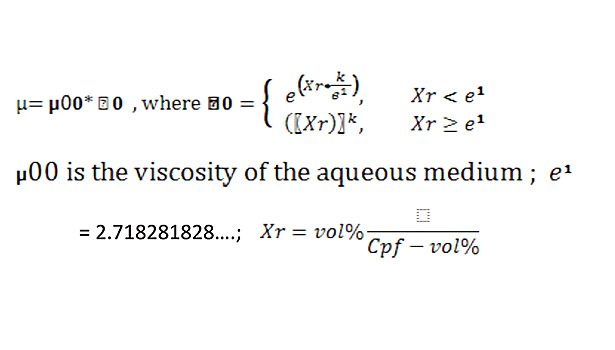Scientists can use computer-aided design programs to prepare waterborne adhesive formulations.

 

Millions of tons of waterborne adhesive formulations are sold each year for the industrial production of myriad manufacturer and consumer products. Applications include paper packaging and converting, construction products, automotive assembly, woodworking, paper and non-woven production, and carpet or textile bonding. The formulator’s art is the creative balancing of economics vs. multiple levels of performance requirements. In this Darwinian marketplace, everything is a trade off, and “survivor” products are fueled by an optimum balance of economics and performance (vs. less ideal, perhaps older, formulations).

 

A major factor to consider in the bonding process is the machining or processability of an adhesive system. The unique characteristics of time, temperature and pressure that are specific to each machine’s process can demand a formulation be designed for each combination of machine and substrate. Research and development efficiency requires that a point of diminishing returns be reached and a formulation be released in order to move on to another high-priority project. Each experiment in this development process may require a lab step to prepare the formulation and pass judgment on the merits of the mixture. Few tools currently exist to help with these experiments, and experience often drives the choices.

 

DEVELOPING FORMULATIONS

Experience and performance can be stored via databases containing lists of chemicals and their percentages within a formulation; unfortunately, this often happens without an understanding of how a formulation works. Judgments can be made from tests whose magnitude of error is as large as the results generated.

 

Armed with a solid foundation and a guiding theory, however, an adhesive formulator may be able to develop quantitative values that describe the formulation’s desired structure and property relationships. In turn, these values can provide a solution that changes experience into a mathematical collection of parameters capable of modeling or even predicting adhesive properties and performance. The result is a virtual adhesives lab.

 

Aqueous adhesive formulations are complex mixtures. An adhesive formulation includes two phases: a collection of various-sized polymer spheres that are dispersed in a thickened aqueous medium. The internal monomer composition of the core of the polymer spheres affects the dry adhesive properties, like adhesion and cohesion. Adhesion is correlated to polymer flow and the wetting of the substrate. The chemical similarity of the polymer to the substrates being bonded and a lower molecular weight are the key parameters in promoting adhesion.

 

Cohesion is boosted by the structural rigidity of the polymer and higher molecular weight, possibly with crosslinking, to produce a lack of flow and resistance to stress. In many cases, for substrates involving cellulose-like paper and wood, the polymer cohesion exceeds the breaking strength of the substrate fiber. As long as fiber tear of the substrate is generated, the adhesive is acceptable.

 

Flowability is dependent upon temperature. Most polymers have a temperature at which they turn from a glassy state with no flow to a plastic state with polymer flow; this is called the glass-transition temperature (Tg). The Tg of a polymer is estimated from the Fox equation, which predicts the Tg from the monomer composition used to produce the polymer. A commercial polymer frequently lists Tg on a technical datasheet.

 

Plasticizers act like soft monomers so that changes in the Tg of the adhesive formulation can be estimated by using the Fox equation (substituting the melt temperature of the plasticizer for the Tg of the raw monomer). Blending 20% on a dry weight basis of a standard benzoate-type plasticizer with a melt temperature of -66°C into a polyvinyl acetate homopolymer with a Tg of 36°C predicts an adhesive with a Tg of +8.29°C.

 

A use temperature of 25°C is 16.71°C above the formulation’s Tg, which puts the adhesive film well into its soft, plastic range without an excessive loss of cohesion. Targeting a formulation’s Tg to a performance target allows a formulator to create families of adhesives with similar types of adhesive and cohesive performance from a variety of raw materials.

 

ADHESIVE SYSTEM RHEOLOGY

The ability to correlate the physical formulation constants of the adhesive composition to performance requirements is more difficult for the wet rheological properties of an adhesive. No widely accepted model exists for predicting the solids/viscosity relationship of soft polymer spheres dispersed in an aqueous medium. Einstein developed the requirements for a model as requiring that:

The form of the equation can be as simple as: 

 

 

For soft polymer spheres, a transitional region occurs where the spheres begin to become compressed and touch each other, around 50 vol % or higher. Individual spheres touch neighboring layers of spheres, influencing the collection as a group. High wet tack is developed in this region. The family of curves is represented in Figure 1. The model scales the solids according to the variable Xr, where Xr = volume solids/(CPF – volume solids). The transitional region is the point where the slope of the power law curve matches the slope of the exponential curve. Mathematically, the transition point is: CPF * e1/(e1+1), which for a CPF = .6839, equates to 50% by volume.

 

The nature of the colloidal layer determines the rheology of the adhesive system. Because the polymer spheres are surrounded by a colloidal layer that protects each particle, the effective volume of a sphere is larger than merely the polymer size. As the colloidal shells are deformed and compressed by each other at volume solids above the transition point, the family of curves is altered by the size of the colloidal shell, which is related to the composition and molecular weight of the protective colloidal system. The additional effect of the added colloidal volume can, in some polymer systems, increase the volume by 15%.

 

The exponent K in the power law curve, which is also the coefficient in the exponential curve, is highly correlated to the average hydrodynamic particle size. The CPF is correlated to the breadth of the particle size distribution. The two statistical parameters, which describe any particle size distribution—namely the mean and the standard deviation—show up in the model as separate variables: the exponent K and the CPF. The particle size distribution and the viscosity of the aqueous medium are all the variables needed to fully describe the solids/viscosity curve of any polymer particle system dispersed in an aqueous medium.

 

Every polymer dispersion has its own set of parameters, µ00, CPF and K, which fix its rheological performance characteristics. These parameters can be found by curve-fitting the viscosities from a short set of experiments to the family of curves. Once the parameters of the polymer dispersion are determined, running experiments on that raw material is no longer necessary. Its rheology can be predicted from the equation.

 

PREDICTING FORMULATION FEATURES

Predicting the characteristics of a formulation before it is created is now extremely easy. For example, when added to a polymer dispersion, plasticizer is absorbed into the polymer particles and causes them to swell. The volume of the plasticizer is absorbed equally by all particles, so the standard deviation of the distribution (i.e., the CPF) is not changed, but the volume solids is raised and the K value increases slightly. Diluting a formulation back with water merely follows the solids/viscosity curve lower as water is added.

 

It is now possible to predict the solids, viscosity, Tg, density, and costs of that plasticized recipe using spreadsheets. Blends of two polymer dispersions are capable of being modeled, as the coefficients can be mathematically averaged according to the proportions of the ingredients. Just as two statistical distributions can be added to create a new distribution of an averaged mean and re-calculated standard deviation, two dispersion curves can be merged together to predict the rheology of any polymer blend. Thus, widely different blends of colloidally stabilized polymers, such as polyvinyl alcohol-stabilized VAE dispersions with blends of surfactant-stabilized VAE polymers can be successfully modeled. As long there are no other effects beyond physical blending, the equation holds.

 

Adding a polyvinyl alcohol cook, an HEC solution or other thickener does not change the particle size distribution; it only changes the viscosity of the suspending medium. When dropping below the volume solids of the transition point, a formulator can just switch to the exponential model. Calculating the new particle/particle factor of the particle distribution in the exponential region accurately predicts the new viscosity of the blend when multiplied by the viscosity of the thickened aqueous phase.

 

Solvents behave like plasticizers and are absorbed by the particles, increasing the mean particle size only. Humectants are dissolved in the water phase, so they alter the aqueous medium’s viscosity. Fillers are particles, so they can be mathematically averaged into the particle size equations to yield a slightly modified CPF and K value. The advantage is that once the coefficients are found, it is no longer necessary to perform any further experiments. The results can be predicted, and only the final formulation need be created.

 

OTHER POSSIBLE PREDICTIONS

Beyond merely predicting of the viscosity of any given formulation, this mathematical model can be used to develop knowledge on the structure/property relationships that are useful in defining industrial processes. The wet tack and setting speed of an adhesive formulation can be related to the rate of rise of the solids/viscosity curve, the K value. As the water is absorbed into a substrate, the volume solids has to rise up the curve until film formation is reached at the CPF. Is the distance of the solids of the formulation from the CPF related to the speed of set? Can sprayability be defined by the transition point?

 

It is known that spheres with sufficient separation from their neighbors spray better than crowded states. Is roller stability also better in the exponential region than the power law region? Can improved raw materials be created? Are new raw materials needed if the formulator can create any combination of particle sizes and aqueous viscosities? These are some of the technical ramifications of the model.

 

Business and commercial opportunities can be addressed as well. Changing raw materials can be simpler, as the equivalency of raw materials can be more firmly developed. Competitive analysis becomes nearly instantaneous, and equivalent formulations are precisely developed. Specifications can be set rationally.

“What-if” feedback can influence future business decisions. Outside of adhesive formulation, the model can possibly help diverse fields from polymer polymerization to medical uses. Aren’t red blood cells just soft concave spheres in an aqueous medium? After all, according to Arthur C. Clarke, “Any sufficiently advanced technology is indistinguishable from magic.”

 

For additional information, contact the author at dhorwat@rcn.com or visit www.winvisq.com.

---

AUTHOR’S ACKNOWLEDGEMENTS

My sincerest appreciation goes to Steve Freeman and the dedicated employees of Accubond Adhesives. They have been extremely receptive to the commercial possibilities and reality of computerized adhesive formulation. Their consistent focus on reproducible quality and an intense desire to achieve the ultimate customer satisfaction makes them perfect partners for this next-generation method of adhesives development.