
The radiated noise and vibration characteristics of manufactured goods are a common concern for most product designers as they strive to provide products that are "whisper quiet." The average consumer has become keenly aware of these issues. The perception that a quieter or smoother-running product is one of higher quality has become a reality to the average consumer today.
Product noise and vibration issues are often generated by the vibrating surfaces of sheet metal components that exhibit low levels of inherent material damping. Source excitation transmitted via an airborne and/or structure-borne path acts to excite dynamic instabilities, or resonances, of these components, often amplifying levels to an excessive amount. This lightly damped, resonant behavior may cause actual high cycle fatigue and failure of critical components or simply result in the presence of unwanted vibration or radiated noise detected by the consumer.
One solution is to increase the level of damping to these components through passive, surface damping treatment. These types of treatments are commonly polymeric in nature and can consist of many forms. Such devices usually include constrained-layer- or free-layer-type damping treatments in which the device is either added onto an existing structure, or components from that structure are manufactured from a new composite material known as damped metal laminate. Roush Anatrol calls such material Dynalam(tm), and it consists of two layers of sheet metal sandwiched together by a thin, energy-absorbing viscoelastic core. The reduced vibration in the product is achieved by converting vibration energy into heat energy dissipated by the viscoelastic material as the part is subjected to cyclic oscillation.
Regardless of the type of damping treatment employed, it is important for those considering such devices to have a basic understanding of viscoelastic material behavior and possess the necessary analytical tools to optimize such noise and vibration control devices for use on specific products and structures.

The Damping Mechanism
A cross-section of a typical laminate sheet is shown in Figure 1(a) and consists of two rigid-metal layers sandwiched together by a polymer, or viscoelastic-core adhesive. As the structure is subject to cyclic vibratory stresses, as shown in Figure 1(b), the individual metal layers move relative to each other, resulting in a shearing action imparted to the core material. This polymer core does more than just bond the laminate together. It also provides the mechanism that creates the damping effect, as these shear strains are converted to heat energy within viscoelastic material.
Viscoelasticity
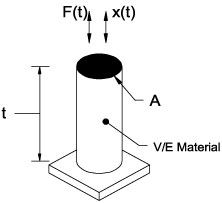
As the name implies, viscoelastic materials possess both elastic and viscous properties. Note the slab of material shown in Figure 2 that is subjected to a cyclic load, F(t), resulting in the corresponding displacement, x(t). For a purely elastic material, all the energy stored in the sample during loading is returned when the load is removed. Furthermore, the displacement of the sample responds immediately, and in-phase, to the cyclic load. Conversely, for a purely viscous material, no energy is returned after the load is removed. The input stress is lost to "pure damping" as the vibratory energy is transferred to internal heat energy.
For all others that do not fall into one of the above extreme classifications, we call viscoelastic materials. Some of the energy stored in a viscoelastic system is recovered upon removal of the load, and the remainder is dissipated by the material in the form of heat. Figure 3 illustrates the relationship between stress and strain for a viscoelastic material subject to cyclic loading.
Material Property Characterization
Another unique characteristic of viscoelastic materials is that their modulus of elasticity is a complex quantity, having both a real and imaginary component. Furthermore, this complex modulus varies as a function of many parameters, most important of which are the temperature and frequency of a given application. It is therefore necessary to establish an accurate and thorough understanding of these parameters in order to design effective damping treatments.
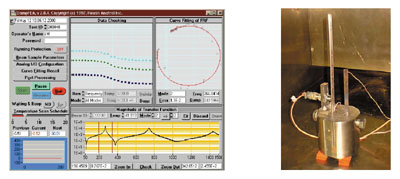
To meet this need, Roush Anatrol has developed a materials-testing laboratory to characterize the complex modulus properties of viscoelastic materials using a variety of experimental techniques. Some of the types of materials evaluated include pressure sensitive adhesives, rubbers, foams, mastics, thermoplastics, enamels, hot melts and structural adhesives. One of the most common methods used is the vibrating-beam technique (ASTM E 756-93), in which the material under test is incorporated into a beam specimen and mounted in a rigid fixture simulating a cantilevered boundary condition. The desired material property information is obtained by measuring the frequency and damping level of the various bending resonances of the cantilever beam and back-calculating the material properties from these composite data. A typical vibrating-beam setup is shown in Figure 4 in which Roush's DampFEA(tm) measurement software is used to acquire and process the test results.
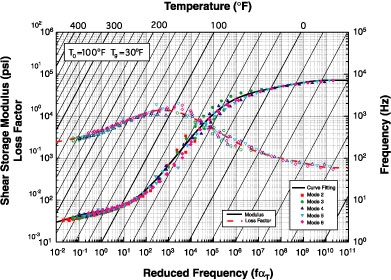
In order to obtain data over a wide temperature and frequency range, the test setup is placed in an environmental chamber and testing is repeated over a broad temperature range for multiple modes of vibration. The output of such testing is to obtain the reduced frequency nomogram, which is the complex modulus of the material independent of the geometry of the test specimen. A typical nomogram plot for a pressure sensitive adhesive is shown in Figure 5.
Shown in the graph are the discrete material-property data collapsed onto one master curve by shifting the data in the frequency domain so as to assume all testing was performed at one specific reference temperature (To). This is possible by utilizing a feature common to viscoelastic materials (known as the Superposition Principle) in which temperature and frequency behavior is inversely proportional. This data is then analytically curve-fit so a simplified equation can be used to represent the actual material properties of any given material as a function of temperature and frequency. This analytical function is now all that is required to interface with search and prediction software utilizing these frequency-temperature-dependent materials.
Analytical Modeling of Damping Treatments
To assist the product designer considering the use of viscoelastic-based surface-damping treatments, such as laminated-metal components, various practical modeling techniques are available that can be used both as a damping prediction and design-optimization tool.
One method commonly used is the Modal Strain Energy (MSE) approach, which utilizes a finite element analysis (FEA) representation of a structure as the basis for modeling the damping effect. This method has been shown to be an accurate predictor of damping levels in structures comprising layers of elastic and viscoelastic elements.1,2 The MSE principle states that the ratio of system loss factor to the material loss factor for a given mode of vibration can be estimated from the ratio of elastic strain energy in the viscoelastic elements to the total strain energy in the model for a given mode.3
Typically, the MSE approach is used in conjunction with an undamped, normal-mode analysis to compute the strain-energy ratio. The strain energies are determined from the relative mode shapes. It is assumed that the viscoelastic properties are linear in terms of the dynamic strain rate.

A Simplified Case Study
One of the many components of a typical automotive engine that contributes to the overall radiated engine noise is the front cover, typically an aluminum die-cast component, as shown in Figure 6. Most front covers possess flat metal sections that have dynamic resonances in the frequency range near 1 kHz. These panel modes exist in a region in which they are easily excited by various engine and accessory-component vibration sources, typically through a structure-borne path. One such mode is illustrated by the modal strain-energy distribution shown in Figure 7 for the driver's side of the cover. These components are lightly damped, and will act to amplify input vibration to excessive levels. To combat this effect, the use of add-on, passive-damping treatments can be employed.

The design optimization process was conducted in two steps. First, the FEA model of the front cover was modified to include solid elements of both the viscoelastic material layer as well as the metal-constraining layer for a proposed coverage region of the damping treatment. Next, multiple analyses were conducted in which the viscoelastic material's shear modulus was varied over a broad range while assuming a viscoelastic loss factor value of unity. This allowed for the determination of the optimum shear modulus required (for the given damping-treatment geometry) to achieve a maximum shear-strain energy ratio of the damping treatment.
The second part of the analysis involved searching the extensive Roush material database to identify candidates that possessed the proper combination of desired stiffness and high damping behavior for the specific temperature and frequency range of interest. Once again, Roush's proprietary software was used to link actual, frequency-temperature-dependent material property data from the database as input to the FEA analysis results
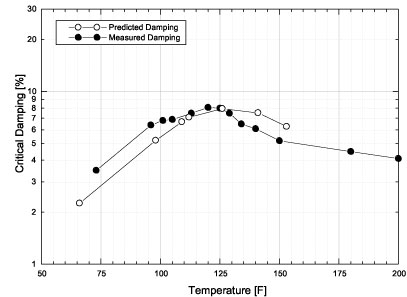
Figure 8 shows the predicted system level damping for one such material as plotted against actual measured values of a prototype damping treatment of identical construction. The damping level of the key panel mode of interest was computed as a function of temperature.
It is important to note that this technique can also be used to perform spatial optimization of the damping treatment, identifying the minimum amount of coverage required to achieve maximum results. Also, the evaluation of multi-layer designs that use a combination of materials to broaden the effective temperature range of the damping treatment can be investigated using this same technique. Obviously, when such geometry changes are made to the FEA model, additional analysis runs are required.
Conclusion
Analytical tools are now available to engineers and product designers challenged with the task of reducing the radiated noise and vibration levels of structures through the use of viscoelastic-based noise and vibration control countermeasures, such as surface damping treatments and laminated metal material. Key to this analysis effort is the proper understanding of viscoelastic material behavior and an accurate characterization of the dynamic properties of the polymeric materials used in these forms of damping devices. Armed with these tools, designers can better and more quickly optimize the effectiveness of these treatments against other competing design parameters.
For more information, visit www.roush.com.
References
- A.D. Nashif, "Control of Noise and Vibration with Damping Materials," Sound and Vibration Magazine, pp. 28-36, July 1983.
- C.D. Johnson, D.A. Kienholtz, L.C. Rogers, "Finite Element Prediction of Damping in Beams with Constrained Viscoelastic Layers," Shock Vibr. Bul., 51(1), pp. 71-81, 1981.
- A.D. Nashif, D.I.G. Jones, J.P. Henderson, Vibration Damping, Wiley Interscience, 1985.


